In a previous post, I discussed how an equation-oriented language like Madonna/STELLA could be translated into Modelica. The point of that post was to demonstrate how constructs in those languages could be mapped to Modelica. But an important caveat in that discussion was that a straight translation would not leverage many of the potential benefits of Modelica.

To take advantage of these benefits, we must transform the flat set of equations we currently have into a more component-oriented representation. This brings several benefits. First, it enables a graphical representation for the various effects, components, sub-systems, etc. Another benefit is in formulating connectors for these components. Modelica supports both causal and acausal semantics in connectors and we will see this automates the process of writing conservation equations. Finally, it allows us to organize the components in ways that represent the domain that we are modeling.

In this post, we'll explore these topics and a few others.

Representation

As mentioned previously, I decided to frame this analysis in terms of metabolism models developed by Kevin Hall at NIH. This defines the types of components we will be building.

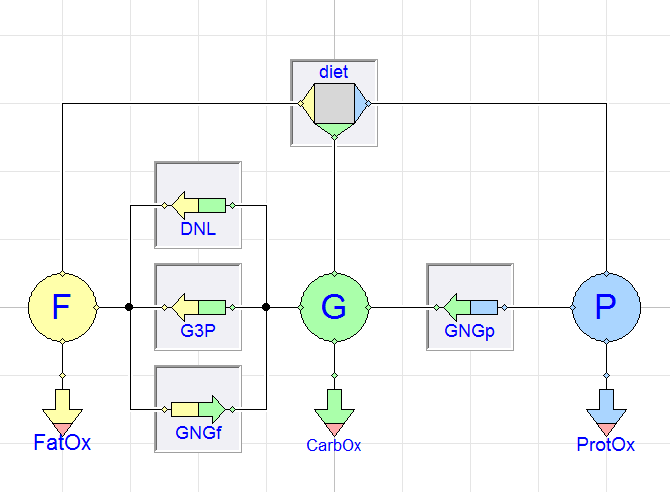
Those models define the interactions between the bodies reserves of fat, glycogen and protein in the body. In his paper outlining these models¹, an overview of the processes involved is presented. The system model I've created for this post greatly resembles that diagram:

He also introduces these equations as the mathematical representation of the system dynamics:

\[ \rho_C { dG \over dt } = CI+ GNG_P + GNG_F - DNL - G3P - CarbOx \]

\[ \rho_F { dF \over dt } = 3M_{FFA} {FI \over M_{TG}} + DNL - FatOx \]

\[ \rho_P { dP \over dt } = PI - GNG_P - ProtOx \]

An important distinction is that the diagram I have presented is a model. Although I have only implemented the top-level interactions for the purposes of this post, it provides a framework for a complete implementation.

Connectors and Conservation

When building a domain specific library in Modelica, the first step is to design the connectors. Connectors in Modelica are used to describe the interactions between components. These connectors generally take two forms.

Causal connectors

Connectors that send and receive information are called causal connectors and the information they carry is qualified in the connector definition by input and output qualifiers to indicate clearly which components are consumers of the information and which are the producers. Such connectors are frequently used in the design of control systems, for example.

However, for the purposes of this post, we will not discuss these connectors in depth. Instead, we will focus on the second type of connector.

Acausal connectors

Acausal connectors are used when we wish to model the flow of anything that can accumulate. In physical modeling, these quantities are almost always a quantity that has a conservation law associated with it (e.g., mass, charge, momentum). However, they can be used for things like raw materials in a process (whether it be manufacturing or metabolism). The big advantage in using acausal formulations for connectors in such systems is the ease with which complex networks of interacting components can be created and the assurance that as material moves from one component to another, none of it is unintentionally "spilled" through sloppy bookkeeping.

For modeling of human metabolism, I have defined three connectors:

connector FatPort "Processes involving fat"
  Modelica.SIunits.Mass F_mass;
  flow Modelica.SIunits.EnergyFlowRate F_rate;
end FatPort;

connector GlycogenPort "Processes involving glycogen"
  Modelica.SIunits.Mass G_mass;
  flow Modelica.SIunits.EnergyFlowRate G_rate;
end GlycogenPort;

connector ProteinPort "Processes involving protein"
  Modelica.SIunits.Mass P_mass;
  flow Modelica.SIunits.EnergyFlowRate P_rate;
end ProteinPort;

These are all quite similar, but the names of the variables on these connectors distinguish each substance type because, while they all have units of mass, it is important to distinguish these to avoid any accidental cross between incompatible connectors.

The X_mass quantity on these connectors represents the accumulated amount of the substance. The X_rate variable represents the flow of energy due to the formation or oxidation of the given substance. With these definitions, we are now in a position to build models for the various effects that create the dynamics of such a system.

Flow and Storage

Now that we have connectors, we can begin building models for the various effects involved in human metabolism. We can group these effects into two types, those that model the storage of a given substance and those that represent the "flow" of that substance (or, more specifically, the energy associated with the transformation of fat, glycogen or protein into each other or into energy).

As far as storage is concerned, the previous equations represent the accumulation of substance via an energy balance equation. In general, each of these has the form:

\[ \rho_X { dX \over dt } = ... \]

where \(\rho_X\) represents the "specific energy" of the substance in question (i.e., how much energy is contained in each unit of mass of \(X\)). The right hand side of the equations represents the various effects that either generate or consume energy by transforming fat, glycogen or protein.

To model the storage side of these equations, I created three different models (using the three previously defined connectors). I will only discuss one of them here, since the equations themselves are nearly identical between them. The model of fat storage is as follows:

model FatStorage
  parameter Modelica.SIunits.SpecificEnergy rho_F;
  Interfaces.FatPort port_a, port_b, port_c;
equation 
  port_b.F_mass = port_a.F_mass;
  port_c.F_mass = port_b.F_mass;
  rho_F*der(port_a.F_mass) = port_a.F_rate + port_b.F_rate + port_c.F_rate;
  annotation (...);
end FatStorage;

I've shown the variable rho_F as a parameter here. This represents the energy density of fat. As such, one might choose to model this (and any of the other \(\rho\) parameters in the equations above) as a physiological constant rather than as an adjustable parameter². In either case, the equations would be the same, only the ability of a user to adjust the parameter would change.

In addition to the rho_F parameter, there are three different ports. A single port would be sufficient. But by incorporating three ports in different locations around the component model, it is possible to create cleaner network diagrams. In other words, the choice of 3 ports is purely cosmetic.

The meat of this model lies in the equation:

rho_F*der(port_a.F_mass) = port_a.F_rate + port_b.F_rate + port_c.F_rate;

This is one of the three main "conservation" equations for the human metabolism system. In effect, the terms on the right hand side represent all the outside influences on this "control volume". Note that it may appear at first glance that this component is somehow limited to three interactions. This is not the case at all. Even with one port, it would be possible to have an infinite number of interactions. The quantity port_a.F_rate represents the net flow of energy into this storage element through that particular port. External to the storage element, there could be any number of connections to that port and the Modelica tool would automatically compute the net contribution.

One last comment about the storage model. If you look carefully, you will note the presence of the text annotation(...). Although I've removed the contents of the annotation, this is an annotation indicating how to render this component model graphically. I left it in simply to point out that this information is present in models. This has the benefit that the appearance is standardized and moves with the model from tool to tool. Most tools hide these annotations when viewing Modelica text simply to keep the source code clean.

Now that we've shown an example of a storage element model, let's look at a model that transforms one quantity into another. To demonstrate this, we will look at the gluconeogenesis from amino acids (\(GNG_P\)) transformation. In the paper, the equation for this process is:

\[ GNG_P = \hat{GNG_P} \left[ \left({ D_P \over \hat{D}_P } \right) - \Gamma_C \left({\Delta CI \over {CI}_b}\right) + \Gamma_P \left({\Delta PI \over {PI}_b} \right) \right] \]

If we translate this model into Modelica, we get something like this:

model GNGpModel 
  "Net rate of gluconeogenesis from amino acid-derived carbon"

  Interfaces.GlycogenPort glycogenPort;
  Interfaces.ProteinPort proteinPort;
protected 
  Real GNG_p;
  Real GNG_p_hat = ...;
  Real D_p = ...;
  Real D_p_hat = ...;
  Real gamma_C = ...;
  Real delta_CI = ...;
  Real CI_b = ...;
  Real gamma_P = ...;
  Real delta_PI = ...;
  Real PI_b = ...;
equation 
  GNG_p = GNG_p_hat*((D_p/D_p_hat)-gamma_C*(delta_CI/CI_b)+gamma_P*(delta_PI/PI_b));
  proteinPort.P_rate = GNG_p;
  glycogenPort.G_rate + proteinPort.P_rate = 0;
end GNGpModel;

This model represents the creation of glycogen from protein. As a result, we need one port to allow us to interact with the glycogen side and the other to allow us to interact with the protein side. There are many intermediate quantities referenced in the paper which I don't show the computations for. Instead, let's focus on the three equations in the equation section:

equation 
  GNG_p = GNG_p_hat*((D_p/D_p_hat)-gamma_C*(delta_CI/CI_b)+gamma_P*(delta_PI/PI_b));
  proteinPort.P_rate = GNG_p;
  glycogenPort.G_rate + proteinPort.P_rate = 0;

The first equation computes GNG_p, the rate at which energy is converted. The next equation computes the rate at which energy from the protein side is consumed. At first glance, you might think that the GNG_p term on the right should have a minus sign in front of it. After all, this process is reducing the amount of protein by transforming it into glycogen. However, it is important to remember that the convention in Modelica is that a flow variable on a connector represents the flow of that quantity into the model it is attached to. In this case, energy flows into this transformation from the protein and flows out into the glycogen storage. So for the protein storage the amount flowing out is negative, but for the transformation itself, it is positive since it is draining the energy from protein storage into itself. Similarly, although the glycogen storage is gaining energy, it is flowing out of the transformation and therefore glycogenPort.G_rate has the opposite sign as proteinPort.P_rate. This kind of "conservation" (that something flows in one port and out another) is represented by the equation:

glycogenPort.G_rate + proteinPort.P_rate = 0;

You will note that the left hand side of this equation is not a variable but an expression. This is because Modelica models contain relationships between variables (i.e., equations) and not assignment statements. The following equations are all equivalent in Modelica:

glycogenPort.G_rate + proteinPort.P_rate = 0;

0 = glycogenPort.G_rate + proteinPort.P_rate;

-glycogenPort.G_rate  = proteinPort.P_rate;

glycogenPort.G_rate  = -proteinPort.P_rate;

The latter of these shows (perhaps more clearly) that these two rates have the opposite sign. However, the form where all flow variables are summed to zero is more common in Modelica as a clear indication that conservation is enforced by the component (i.e., the zero represents the amount of storage in the component).

If we revisit the original equations, we see something interesting about the structure of those equations and the equations of our components:

\[ \rho_C { dG \over dt } = ... + GNG_P + ... \]

\[ \rho_P { dP \over dt } = ... - GNG_P + ... \]

The terms on the left represent the behavior of the storage model. The terms on the right represent the terms of a flow model. Furthermore, the terms on the right have a different sign in each equation. This indicates a conversion or transformation from one type of substance to another. Other representations are possible as well, e.g.,

\[ \rho_C { dG \over dt } = CI + ... - CarbOx \]

\[ \rho_P { dP \over dt } = PI + ... - ProtOx \]

In these cases, we have "source" terms (\(CI\) and \(PI\) represent the intake of these substances through diet) and "sink" terms ((\CarbOx\) and \(ProtOx\) represent the oxidation of these substances into energy for physical activity). All of these various effects can be represented using just the simple connector definitions shown previously.

Networks and Architectures

Apart from the nice graphical appearance, you might wonder why this is better than the approach I described previously.

First, we can create arbitrarily complex networks of interactions. By isolating the various affects (storage, oxidation, transformation, intake), we can compose models in a more robust and less fragile way. This has the benefit of keeping each individual model relatively simple (as we have seen so far) but allowing us to combine them in an intuitive way to demonstrate complex interactions. Although we haven't covered it in this post, we can compose complex hierarchies of components and interactions.

Another big benefit here is of replaceability. Let us revisit our original system model diagram:

Note the "sunken" appearance around some of the blocks in the system? This is a graphical indication that I've marked those components as replaceable. The replaceable keyword is an indication that a model can be extended and modified. It allows you to define an invariant architecture for the model (so that all connections/interactions are fixed) but with the freedom to "fill in the blanks" regarding the behavior of individual components. Typically, such flexibility is used to substitute different levels of detail for a given "blank". But in the context of metabolism modeling, the same mechanism could be used to, for example, substitute different diets (the component at the top of the diagram) or even to capture the metabolic differences between genders or populations.

These types of features bring to bear much of the thinking in recent decades about how to properly build and manage software. It may not be apparent at first why such "complexity" is necessary but the reality is that models are software. As such, there is no reason models and their developers shouldn't benefit from proven techniques and ideas when building and managing models. But furthermore, it is important for the modeling community to recognize that viewing models as software is necessary in order to scale the process of building and managing models to the level that software has achieved.

Conclusion

This is a rich topic and while I've only scratched the surface, I've probably simultaneously and paradoxically presented an overwhelming amount of information at the same time.

My goal was to show how a given domain (even those outside engineering) that contains principles related to the movement, transformation and storage of "stuff"³ can be mapped into a domain specific library of Modelica components. Modelica not only provides language features for representing the graphics and behaviors in such systems but it provides language features designed to bring the scalability of software engineering to the process of building and managing mathematical models.